KD 1.6 GRADIEN YANG SEJAJAR DAN TEGAK LURUS

Beberapa sifat gradien yang perlu kita ketahui antara lain gradien garis yang sejajar sumbu x, gradien garis yang sejajar sumbu y, gradien garis yang saling sejajar, dan gradien garis yang saling tegak lurus.

Gradien Garis yang Sejajar Sumbu x

Perhatikan gambar berikut ini.

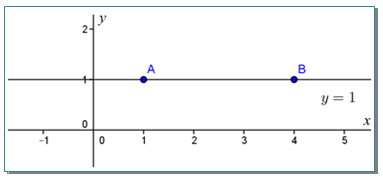
Persamaan garis yang sejajar sumbu x berbentuk y = k. Pada gambar di atas dicontohkan persamaannya adalah y = 1 yang melalui titik A (1, 1) dan B (4, 1). Gradien garis y = 1 dapat ditentukan dengan rumus gradien garis melalui dua titik.

Ini berarti:
(1, 1) → x1 = 1 dan y1 = 1
(4, 1) → x2 = 4 dan y2 = 1

m=y2–y1x2–x1=1–14–1=03=0

Dengan demikian, gradien semua garis yang sejajar sumbu x adalah 0.

Gradien Garis yang Sejajar Sumbu y

Perhatikan ilustrasi berikut ini.

Persamaan garis yang sejajar sumbu y berbentuk x = k. Pada gambar di atas dicontohkan persamaannya adalah x = 1 yang melalui titik A (1, 1) dan B (1, 2). Gradien garis y = 1 dapat ditentukan dengan rumus gradien garis melalui dua titik.

Ini berarti:
(1, 1) → x1 = 1 dan y1 = 1
(1, 2) → x2 = 1 dan y2 = 2

m=y2–y1x2–x1=2–11–1=10=∞

Dengan demikian, gradien semua garis yang sejajar sumbu y adalah ∞ atau tidak terdefinisi.

Contoh 1

Gradien garis yang melalui titik (3, 10) dan (9, 10) adalah ....

Penyelesaian:

Diketahui garis yang melalui titik (3, 10) dan (9, 10).

Perhatikan bahwa ordinat (y) kedua titik sama yaitu 10, sehingga garis ini sejajar sumbu x dan memiliki persamaan y = 10.

Gradien semua garis yang sejajar sumbu x adalah 0.

Jadi, gradien garis yang melalui titik (3, 10) dan (9, 10) adalah 0.

Soal ini juga dapat ditentukan dengan menggunakan rumus gradien garis yang melalui 2 titik yaitu:

m=y2–y1x2–x1=10–109–3=06=0

Gradien Dua Garis Sejajar

Diketahui persamaan garis y = 2x. Persamaan garis baru yang sejajar dengan garis tersebut dapat diperoleh dengan menggeser ke atas atau ke bawah searah sumbu y. Misalkan persamaan y = 2x digeser sebanyak 3 satuan ke atas sehingga diperoleh garis yang sejajar dengannya yaitu y = 2x + 3.

       Misalkan diketahui y1 = 3x + 10 dan y2 = 3x -4. Kedua garis ini merupakan garis yang sejajar karena memilki koefisien x yang sama yaitu 3. Dengan konsep gradien pada garis y =mx + c diperoleh m1 = m2 = 3. Dengan demikian, jika garis y1 = m1x + c sejajar dengan garis y2= m2x + d, maka berlaku m1 = m2, dengan kata lain setiap garis yang sejajar memiliki gradien yang sama.

Contoh 2

Diketahui 2 buah garis yaitu garis k dan l. Garis k melalui (1, 2) dan (-1, 6), sedangkan garis lmelalui (a, 4) dan (0, 2). Jika garis k sejajar dengan garis l, maka tentukan nilai a.

Penyelesaian:

Diketahui:
garis k melalui (1, 2) dan (-1, 6)
garis l melalui (a, 4) dan (0, 2).

Misalkan:
gradien garis k = mk
gradien garis l = ml

Gradien garis k dan garis l dapat ditentukan dengan rumus gradien melalui 2 titik.

Untuk garis k:
(1, 2) → x1 = 1 dan y1 = 2
(-1, 6) → x2 = -1 dan y2 = 6

mk=y2–y1x2–x1=6–2−1–1=4−2=−2

Untuk garis l:
(a, 4) → x1 = a dan y1 = 4
(0, 2) → x2 = 0 dan y2 = 2

ml=y2–y1x2–x1=2–40–a=2a

Oleh karena garis k sejajar dengan garis l, maka:
mk=ml
⇔ −2=2a
⇔ a=2−2=−1

Jadi, nilai a adalah -1.

Gradien Dua Garis yang Tegak Lurus

Perhatikan gambar dibawah ini.

Dari gambar di atas diketahui bahwa garis y1=−12x dan y2 = 2x saling berpotongan tegak lurus karena sudut yang dibentuk oleh kedua garis adalah 90⁰. Dengan menggunakan konsep gradien garis y = mx + c diperoleh m1=−12 dan m2 = 2, sehingga:

m1.m2=−12.2=−1

Dengan demikian, jika garis y1 = m1x + c tegak lurus dengan garis y2 = m2x + d, maka berlakum1 . m2 = -1, dengan kata lain hasil kali gradien dua garis yang saling tegak lurus adalah -1.

Contoh 3

Diketahui garis y = 3x + 5 tegak lurus garis y = ax + 10. Tentukan nilai a.

Penyelesaian:

Misalkan:
gradien garis y = 3x + 5 = m1
gradien garis y = ax + 10 = m2

Dengan menggunakan konsep gradien garis y = mx + c diperoleh m1 = 3 dan m2 = a.

Oleh karena kedua garis tersebut saling tegak lurus, maka berlaku m1 . m2 = -1, sehingga:

3a=−1⇔a=−13

Jadi, nilai a adalah −13.