DAERAH HIMPUNAN PENYELESAIAN SISTEM PERTIDAKSAMAAN KUADRAT DUA VARIABEL

Sebelumnya kalian telah mempelajari tentang sistem persamaan kuadrat dua variabel, dan cara menyelesaikan masalah nyata yang model matematikanya berkaitan dengan sistem persamaan tesebut. Dalam topik ini kalian akan belajar tentang cara menentukan Daerah Himpunan Penyelesaian (DHP) sistem pertidaksamaan kuadrat dua variabel.

Sistem pertidaksamaan kuadrat dua variabel adalah kumpulan 2 atau lebih pertidaksamaan yang mengandung paling sedikit satu persamaan berderajat dua dalam dua variabel.

Berikut ini adalah beberapa contoh sistem pertidaksamaan kuadrat dua variabel :

Sistem pertidaksamaan 1

y ≤ x2
y > x + 2

Sistem pertidaksamaan 2

y ≤ -x2 + 2x + 1
y ≥ x2 + x + 2

Penyelesaian dari sebuah sistem pertidaksamaan merupakan irisan dari pertidaksamaan-pertidaksamaan yang membentuk sistem tersebut, biasanya lebih mudah ditunjukkan dalam bentuk grafik. Grafik penyelesaian dari sistem pertidaksamaan adalah himpunan titik-titik yang mewakili semua penyelesaian pertidaksamaan dalam sistem pertidakamaan tersebut, dan himpunan titik tersebut dinamakan Daerah Himpunan Penyelesaian (DHP). DHP ini dibatasi oleh kurva pembatas yang dibentuk dari pertidaksamaan-pertidaksamaan dalam sistem tersebut.

Kurva/garis pembatas dibuat dengan aturan sebagai berikut :
• Pertidaksamaan yang memuat tanda < atau >, kurva pembatasnya digambarkan dengan garis putus-putus
• Pertidaksamaan yang memuat tanda ≤ atau ≥, kurva pembatasnya digambarkan dengan garis penuh

Bagian yang merupakan daerah himpunan penyelesaian dari suatu pertidaksamaan biasanya diberi arsiran, untuk membedakannya dengan yang bukan DHP.

Contoh

Gambarlah daerah himpunan penyelesaian sistem persamaan berikut :

y ≥ x2
y ≤ 2x+3

Penyelesaian

Kurva Pembatas : y = x2

Untuk menggambar kurva di atas, dapat diambil beberapa nilai absis (x), kemudian kita hitung nilai ordinatnya (y), sehingga diperoleh sebuah titik. Selanjutnya, titik-titik yang diperoleh kita hubungkan.

x = -2 => y = 4 => (-2,4)
x = -1 => y = 1 => (-1,1)
x = 0 => y = 0 => (0,0)
x = 1 => y = 1 => (1,1)
x = 2 => y = 4 => (2,4)

Garis Pembatas : y=2x+3

Untuk menggambar garis di atas, dapat diambil beberapa nilai absis (x), kemudian kita hitung nilai ordinatnya (y), sehingga diperoleh sebuah titik. Selanjutnya, titik-titik yang diperoleh kita hubungkan.

x = -2 => y = -1 => (-2,-1)
x = -1 => y = 1 => (-1,1)
x = 0 => y = 3 => (0,3)
x = 1 => y = 5 => (1,5)
x = 2 => y = 7 => (2,7)

Titik Potong

Titik potong diperoleh dengan cara mensubtitusikan persamaan y = x2 ke dalam persamaan y = 2x + 3, sehingga diperoleh :
x2 = 2x + 3
<=> x2 - 2x - 3 = 0
<=> (x-3)(x+1) = 0
<=> x = 3 atau x = -1

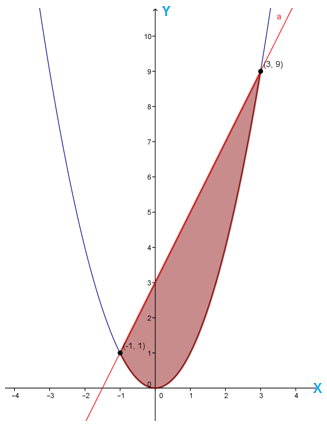
Jika x = -1 maka y = 1 dan jika x = 3 maka y =9.
Dengan demikian titik potongnya adalah (-1,1) dan (3,9).

Daerah Himpunan Penyelesaian

Untuk menentukan daerah himpunan penyelesaian, kita perlu melakukan uji titik.

y ≥ x2

Ambil sebarang titik, misal titik (0,1). Karena x2 = 0, maka titik (0,1) memenuhi pertidaksamaan y ≥ x2, sehingga daerah penyelesaian berada diatas kurva y = x2.

y ≤ 2x + 3

Ambil sebarang titik, misal titik (0,1). Karena 2x+3 =3, maka titik (0,1) memenuhi pertidaksamaan y ≤ 2x + 3 sehingga daerah penyelesaian berada dibawah garis y = 2x + 3.

Dengan demikian, daerah himpunan penyelesaian dari sistem pertidaksamaan di atas adalah :