SIFAT-SIFAT PERSAMAAN TRIGONOMETRI

Dalam topik ini, kalian akan belajar mengenai sifat-sifat persamaan trigonometri. Apakah kalian masih ingat dengan materi trigonometri yang telah kalian pelajari di matematika wajib?

Gunakan pengetahuan kalian akan materi tersebut, sehingga kalian dapat dengan mudah memahami materi sifat-sifat trigonometri ini.

Persamaan Identitas Trigonometri

Persamaan identitas trigonometri yang paling sering digunakan adalah sebagai berikut :

• cos2 x + sin2 x = 1
• 1 + tan2 x = sec2 x
• 1 + cot2 x = cosec2 x

Contoh 1 :

Buktikan identitas trigonometri 1 + tan2 x = sec2 x !

Penyelesaian :

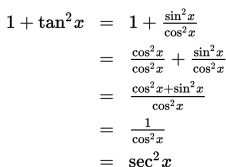
(terbukti)

Contoh 2 :

Buktikan identitas trigonometri berikut!

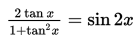
Penyelesaian :

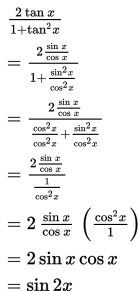
(terbukti)

Persamaan Trigonometri Sederhana

Sifat-sifat persamaan trigonometri sederhana untuk sinus, cosinus, dan tangen adalah sebagai berikut :

1. Bentuk sin x = sin p

Bentuk di atas mempunyai dua macam penyelesaian, yaitu :

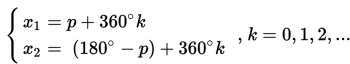
2. Bentuk cos x = cos p

Bentuk di atas mempunyai dua macam penyelesaian, yaitu :

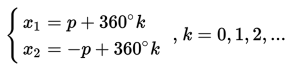
3. Bentuk tan x = cos p

Bentuk di atas mempunyai penyelesaian sebagai berikut :

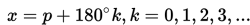
Contoh 3:

Tentukan himpunan penyelesaian dari sin 2x = ½ jika 0∘ ≤ x ≤ 360∘ !

Penyelesaian :

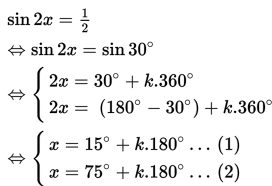
Persamaan (1)

• Jika k = 0 maka x1 = 15o
• Jika k = 1 maka x2 = 195o

Persamaan (2)

• Jika k = 0 maka x3 = 75o
• Jika k = 1 maka x4 = 255o

Jadi, himpunan penyelesaiannya adalah {15o, 75o, 195o, 255o}.

Contoh 4 :

Tentukan himpunan penyelesaian dari tan (4x - π) = 1 !

Penyelesaian :

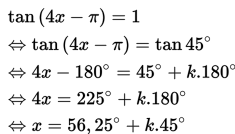
• Jika k = 0 maka x1 = 56,25∘
• Jika k = 1 maka x2 = 101,25∘
• Jika k = 2 maka x3 = 146,25∘
• Jika k = 3 maka x4 = 191,25∘
• Jika k = 4 maka x5 = 236,25∘
• Jika k = 5 maka x6 = 281,25∘
• Jika k = 6 maka x7 = 326,25∘
• Jika k = 7 maka x8 = 371,25∘ = 11,25∘

Jadi, himpunan penyelesaiannya adalah 
{ 11,25∘ , 56,25∘ , 101,25∘ , 146,25∘ , 191,25∘ , 236,25∘ , 281,25∘ , 326,25∘ }.