Unsur dan Luas Permukaan Tabung
Pernahkah kalian memperhatikan kaleng cat, kaleng susu, atau drum tempat minyak. Benda-benda tersebut memiliki bentuk yang hampir sama.

Selain benda-benda tersebut, beberapa wadah benda cair juga mempunyai bentuk yang sama yaitu berbentuk tabung. Apa itu tabung? Tabung merupakan salah satu bangun ruang dengan sisi berbentuk lengkung yang disebut bangun ruang sisi lengkung. Mari mempelajari lebih dalam tentang tabung.
Unsur Tabung
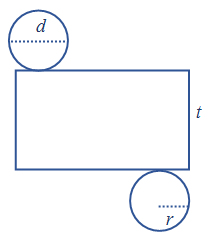
Tabung dibentuk dari dua buah lingkaran yang menjadi alas dan tutupnya, serta selimut yang menjadi sisi tegaknya. Dua buah lingkaran yang saling berhadapan tersebut memiliki besar dan luas yang sama. Sisi tegak tabung berupa persegipanjang yang dilengkungkan mengikuti sisi alas dan tutupnya. Dengan demikian, tabung terdiri dari tiga sisi yang merupakan sisi alas, sisi tegak, dan sisi tutupnya. Tabung memiliki dua rusuk yang membentuk sisi alas dan sisi tutupnya.

Perhatikan gambar tabung di atas. Pada gambar tersebut, r merupakan jari-jari alas dan tutup tabung yang disebut dengan jari-jari tabung , sedangkan t merupakan jarak antara alas dan tutup tabung yang dikenal dengan tinggi tabung. Nilai r juga dapat ditentukan dengan menggunakan diameter (d) yaitu r=12d . Jika tabung diiris pada rusuknya, maka akan membentuk jaring-jaring tabung sebagai berikut.
Dari jaring-jaring di atas, diketahui bahwa tabung terdiri dari dua lingkaran yang kongruen dan sisi tegak yang merupakan sebuah persegipanjang. Konsep ini akan digunakan untuk menentukan rumus luas permukaan tabung.
Luas Permukaan Tabung
Luas permukaan tabung adalah jumlah luas bangun datar yang menutupi seluruh permukaan tabung. Permukaan tabung terdiri dari dua lingkaran dan satu persegipanjang. Luas permukaannya ditentukan dengan menjumlahkan dua kali luas lingkaran dan luas persegipanjang. Persegipanjang tersebut memiliki panjang yang merupakan keliling lingkaran dan tingginya yang merupakan tinggi tabung. Jika panjang jari-jari alas dan tutup adalah rserta tinggi tabung adalah t, maka luas permukaan tabung dapat ditentukan sebagai berikut:
Luas permukaan tabung adalah jumlah luas bangun datar yang menutupi seluruh permukaan tabung. Permukaan tabung terdiri dari dua lingkaran dan satu persegipanjang. Luas permukaannya ditentukan dengan menjumlahkan dua kali luas lingkaran dan luas persegipanjang. Persegipanjang tersebut memiliki panjang yang merupakan keliling lingkaran dan tingginya yang merupakan tinggi tabung. Jika panjang jari-jari alas dan tutup adalah rserta tinggi tabung adalah t, maka luas permukaan tabung dapat ditentukan sebagai berikut:
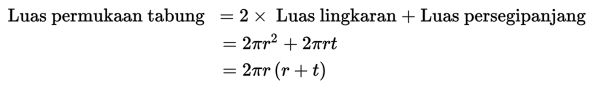
Dengan demikian, luas permukaan tabung dapat ditentukan dengan rumus:
Lp = 2πr (r + t)
Keterangan:
r = jari-jari
t = tinggi tabung
π =227 = 3,14
r = jari-jari
t = tinggi tabung
π =
Contoh
Sebuah tabung memiliki jari-jari 10 cm dan tinggi 20 cm.
Tentukan :
Tentukan :
- luas alas dan tutupnya
- luas sisi tegaknya (luas selimut)
Penyelesaian:
Diketahui:
jari-jari tabung = r = 10 cm
tinggi tabung = t = 20 cm
jari-jari tabung = r = 10 cm
tinggi tabung = t = 20 cm
- Luas alas dan tutup tabung
Alas dan tutup tabung berbentuk lingkaran yang saling kongruen, sehingga luasnya dapat ditentukan menggunakan luas lingkaran.

- Luas sisi tegak tabung
Sisi tegak tabung berbentuk persegipanjang dengan panjang merupakan keliling lingkaran dan lebarnya merupakan tinggi tabung.

