DAERAH PENYELESAIAN PERTIDAKSAMAAN IRRASIONAL

Dalam topik sebelumnya, kita telah mempelajari mengenai pertidaksamaan pecahan. Dalam topik ini, kita akan mempelajari daerah penyelesaian pertidaksamaan irrasional. Sebelum kita mempelajari konsep pertidaksamaan irrasional mari kita lihat arti dari bilangan irrasional.

Bilangan irrasional adalah bilangan yang tidak dapat dinyatakan dalam bentuk a/b dimana a dan b adalah bilangan bulat dan b ≠ 0). Salah satu contoh bilangan irrasional yang paling populer adalah bentuk akar.

Setelah kita mempelajari arti dari bilangan irrasional marilah kita mulai dengan bentuk pertidaksamaan irrasional.

1. Pertidaksamaan Irrasional

Bentuk umum pertidaksamaan irrasional adalah sebagai berikut :

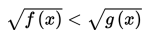
Bentuk diatas disebut sebagai bentuk pertidaksamaan irrasional karena variabelnya ada tanda akar dan keduanya dihubungkan dengan tanda pertidaksamaan (<, >, ≤, ≥).

Perlu diingat pula bahwa f(x) ≥ 0 dan g(x) ≥ 0

2. Daerah Penyelesaian Pertidaksamaan Irrasional

Untuk menyelesaikan pertidaksamaan irrasional, diperlukan langkah – langkah untuk menyelesaikannya yaitu sebagai berikut:
1. Kuadratkan kedua ruas pertidaksamaan, kemudian selesaikan
2. Tentukan syarat bahwa bentuk akar harus selalu bernilai positif atau sama dengan 0 (≥ 0)
3. Tentukan interval irisan yang memenuhi pada langkah pertama dan kedua

Dengan demikian, jika :

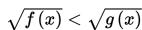
maka langkah – langkah penyelesaiannya adalah :
1. f(x) < g(x) ( ruas kiri dan kanan dikuadratkan) kemudian selesaikan 
2. f(x) ≥ 0 dan g(x) ≥ 0
3. Tentukan interval irisan

Untuk lebih jelasnya, mari kita mencermati contoh soal berikut ini.

Contoh

Tentukan nilai x yang memenuhi pertidaksamaan :

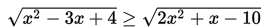
Penyelesaian:

Langkah 1 : 
Kuadratkan kedua ruas pertidaksamaan kemudian selesaikan pertidaksamaan tersebut

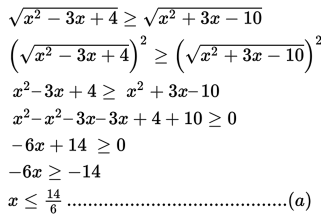
Langkah 2 :

Tentukan syarat bahwa bentuk akar harus selalu bernilai positif atau sama dengan 0.

(1)

x2 - 3x + 4 ≥ 0 <=> (x - 4) (x + 1) ≥ 0 <=> x = 4 dan x = -1

Dengan mengambil titik uji x = 0, diperoleh :
x2 - 3x + 4 > 0

Garis bilangan :

Penyelesaiannya adalah -1 ≤ x ≤ 4 ……………………..(b)

(2)

x2 + 3x - 10 ≥ 0 <=> (x + 5) (x – 2) ≥ 0 <=> x = - 5 dan x = 2

Dengan mengambil titik uji x = 0, diperoleh x2 + 3x - 10 < 0

Garis bilangan :

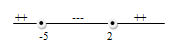
Penyelesaiannya adalah x ≤ -5 atau x ≥ 2 …………………………(c)

Dari hasil (a), (b) dan (c) dapat kita simpulkan bahwa :

1) x ≤ 14/6
2) - 1 ≤ x ≤ 4
3) x≤-5 atau x≥2

dengan garis bilangan sebagai berikut :

Penyelesaiannya : gabungan irisan interval syarat (a), (b) dan (c)

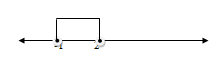
Jadi, penyelesaiannya adalah -1 ≤ x ≤ 2