MODEL MATEMATIKA DARI MASALAH PROGRAM LINEAR

Pada topik sebelumnya, kita telah membahas tentang penyelesaian sistem pertidaksamaan linear dua variabel. Kali ini, kita akan belajar membuat model matematika dari suatu permasalahan program linear. 

       Sebelum kita membahas lebih lanjut, apakah kalian masih ingat dengan sistem pertidaksamaan linear dua variabel pada pembahasan sebelumnya? Bagaimana bentuknya? Ya, pertidaksamaan linear dua variabel merupakan suatu kalimat matematika yang memuat tanda ketidaksamaan (≤, < ,≥, >) dan terdiri dari dua buah variabel, sedangkan sistem pertidaksamaan linear dua variabel adalah suatu sistem yang terdiri dari dua atau lebih pertidaksamaan linear dua variabel. 
Contoh sistem pertidaksamaan linear:
                                                        x−y≥0x+y≤−1x≥0y≥0

       Jika pada topik sebelumnya pertidaksamaan linear langsung diberikan pada soal, kali ini kita akan belajar memodelkan sendiri pertidaksamaan yang ada dalam sistem pertidaksamaan linear tersebut. Kalimat matematika berupa pertidaksamaan linear dua variabel akan dimodelkan berdasarkan permasalahan program linear dalam kehidupan sehari-hari. Lalu, bagaimanakah mengubah permasalahan ke dalam kalimat matematika? Oleh karena itu, perhatikanlah materi ini dengan baik.

Sebagaimana yang telah kita ketahui, penyelesaian masalah yang berkaitan dengan program linear biasanya mengandung variabel. Oleh karena itu, langkah pertama dalam menyelesaikan masalah program linear adalah dengan menerjemahkan permasalahan tersebut ke dalam bahasa/model matematika yang membentuk suatu sistem pertidaksamaan. Apa itu model matematika?

Untuk mengetahui apa saja langkah-langkah dalam menentukan model matematika dari suatu permasalahan linear, perhatikanlah contoh berikut.

Perhatikan kalimat dibawah ini.

Ibu ingin menyiapkan kue untuk acara keluarga. Ibu akan membeli dua jenis kue yang jumlahnya paling sedikit 20 buah.

Kalimat di atas dapat ditulis dengan bentuk pertidaksamaan dua variabel.

Adapun langkah-langkah dalam menentukan model matematika dari suatu permasalahan program linear adalah sebagai berikut.

• Membuat pemisalan

          Kita tuliskan pemisalan dari objek pada permasalahan dengan sebuah variabel.
          Pada contoh di atas, misalkan:

          x$x$ = banyak kue jenis pertama yang dibeli Ibu; dan
          y$y$ = banyak kue jenis kedua yang dibeli Ibu.

• Mengganti kalimat yang menyatakan jumlah dengan tanda ketidaksamaan
                                                                                                                                                                    Pada contoh di atas, " Ibu akan membeli dua jenis kue yang jumlahnya paling sedikit 20 buah ", artinya Ibu akan membeli kedua jenis kue tersebut yang jumlahnya lebih dari atau sama dengan 20. Ini berarti tanda ketidaksamaan yang digunakan adalah ≥20
• Menuliskan bentuk pertidaksamaan dari permasalahan tersebut                                                                                                                                                                    Pada contoh di atas, dapat diketahui bahwa kue jenis pertama ditambah kue jenis kedua jumlah paling sedikit adalah 20. Jadi, bentuk pertidaksamaan dari kalimat tersebut adalah x+y≥20.

Untuk memudahkan kita dalam memodelkan permasalahan program linear ke dalam kalimat matematika berupa pertidaksamaan, pahamilah tabel berikut ini.

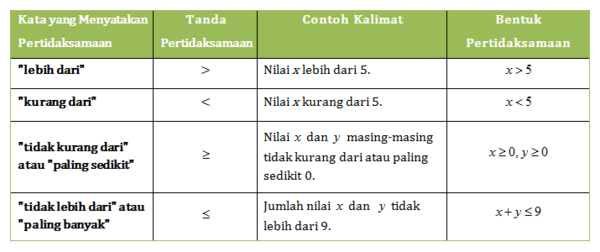
Sekarang, mari kita berlatih membuat model matematika dari suatu permasalahan program linear dengan memperhatikan beberapa contoh soal berikut ini.

Contoh Soal

Contoh Soal 1

Vani dan teman-temannya menjual es buah dan es teh pada acara festival kuliner di sekolahnya. Mereka menjual es buah dengan harga Rp6.500,00 dan es teh seharga Rp5.000,00. Buatlah model matematika dari kondisi di atas, jika:

a.     mereka berhasil menjual sekurang-kurangnya 35 gelas minuman; dan

b.     pendapatan mereka tidak kurang dari Rp250.000,00

 Penyelesaian 

Misalkan:
banyaknya es buah yang terjual adalah x; dan

banyaknya es teh yang terjual adalah y

a.     Mereka berhasil menjual sekurang-kurangnya 35 gelas minuman

Ini berarti, banyaknya es buah yang terjual ditambah banyaknya es teh yang terjual lebih dari atau sama dengan 35. 
Jadi, bentuk pertidaksamaannya adalah x+y≥35.

b.     Pendapatan mereka tidak kurang dari Rp250.000,00

Diketahui harga es buah adalah Rp6.500,00 dan harga es teh adalah Rp5.000,00. Pendapatan diperoleh dari harga es buah dikali banyaknya es buah yang terjual, ditambah harga es teh dikali banyaknya es teh yang terjual. Kata "tidak kurang dari Rp250.000,00" berarti lebih atau sama dengan Rp250.000,00. 
Jadi, bentuk pertidaksamaannya adalah 6500x+5000y≥250.000.

Contoh Soal 2 

Bu Rini adalah seorang penjahit baju wanita. Ia menerima beberapa pesanan baju dengan dua model yang berbeda. Model A membutuhkan 1 meter kain batik dan 1 meter kain satin. Model B membutuhkan 2 meter kain batik dan 1 meter kain satin. Bu Rini memiliki persediaan 10 meter kain batik dan 6 meter kain satin. Buatlah model matematika dari kondisi tersebut.

Penyelesaian 

Misalkan: 
a adalah banyak baju model A yang akan dibuat oleh Bu Rini; dan
b adalah banyak baju model B yang akan dibuat oleh Bu Rini.

• Setiap baju model A membutuhkan 1 meter kain batik. Setiap baju model B membutuhkan 2 meter kain batik. Kain batik yang tersedia adalah 10 meter.

Sebanyak a baju model A memerlukan a dikali 1 meter kain batik = a
Sebanyak b baju model B memerlukan b dikali 2 meter kain batik = 2b
Jumlah kain batik yang dibutuhkan untuk membuat baju model A dan model B adalah a+2bmeter.
Oleh karena kain batik yang tersedia hanya 10 meter, maka a+2b tidak boleh lebih dari 10 meter, sehingga pertidaksamaan yang dapat dibentuk adalah:
a+2b≤10,dengan a,bϵ bilangan bulat positif.

• Setiap baju model A dan model B masing-masing membutuhkan 1 meter kain satin. Kain satin yang tersedia adalah 6 meter.

Sebanyak a baju model A memerlukan adikali 1 meter kain satin = a
Sebanyak b baju model B memerlukan b dikali 1 meter kain satin = b
Jumlah kain satin yang dibutuhkan untuk membuat baju model A dan model B adalah a+b$a+b$meter.
Oleh karena kain satin yang tersedia hanya 6 meter, maka a+btidak boleh lebih dari 6 meter, sehingga pertidaksamaan yang dapat dibentuk adalah:
a+b≤6 ,dengan a,bϵ bilangan bulat positif.

Jadi, model matematika pada permasalahan di atas adalah:
a+2b≤10, dengan a,bϵ bilangan bulat positif 
a+b≤6, dengan a,bϵ bilangan bulat positif

Model matematika di atas dapat juga dinyatakan dengan,
a+2b≤10a+b≤6a≥0b≥0