PERTIDAKSAMAAN IRRASIONAL

Perhatikan pertidaksamaan-pertidaksamaan berikut ini :

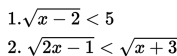
Pertidaksamaan di atas adalah pertidaksamaan Irrasional, yaitu pertidaksamaan yang variabelnya terdapat di dalam tanda akar. Mari kita ingat kembali bahwa suatu fungsi irrasional bernilai real atau terdefinisi jika bagian di dalam tanda akar dari fungsi irrasional itu positif atau nol.

Jadi, fungsi irasional :

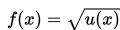
bernilai real atau terdefinisi jika dan hanya jika u(x) ≥ 0.

Bentuk umum Pertidaksamaan Irrasional adalah :

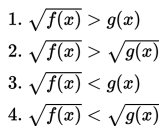
(tanda > dan < dapat diganti ≥ dan ≤ )

Cara Menyelesaikan Pertidaksamaan Irrasional

Untuk menyelesaikan pertidaksaman irasional, yang perlu dilakukan adalah mengubah pertidaksamaan irasional tersebut menjadi 
pertidaksamaan ekuivalen yang tidak memuat tanda akar lagi, yaitu dengan cara mengkuadratkan kedua ruas.

Langkah-Langkah Menyelesaikan Pertidaksamaan Irrasional

Jika diberikan pertidaksamaan Irrasional :

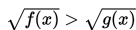
maka penyelesaiannya harus memenuhi syarat berikut :
1) f(x) ≥ 0 
2) g(x) ≥ 0 
3) f(x) ≥ g(x)

Contoh 1

Carilah penyelesaian dari pertidaksamaan irrasional berikut ini :

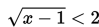
Jawab

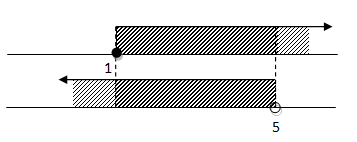
Dengan menggabungkan hasil i dan ii, maka diperoleh 1 ≤ x < 5

Contoh 2

Carilah penyelesaian pertidaksamaan irrasional berikut ini :

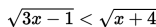
Jawab

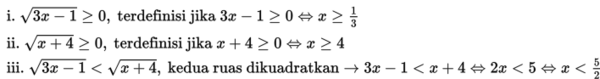
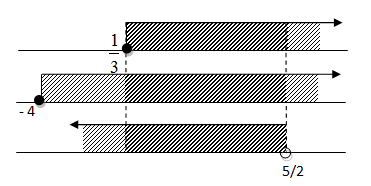
Dengan menggabungkan hasil i, ii, dan iii diperoleh 1/3 ≤ x < 5/2